刚刚，deepseek低调开源，金牌级模型！

刚刚，DeepSeek又悄悄开源了DeepSeek-Math-V2：迈向可自证的数学推理。

model、paper都已开源。

DeepSeekMath-V2 展现出强大的定理证明能力：在 IMO 2025、CMO 2024 上达到金牌线，并在 Putnam 2024 上以扩展测试时计算斩获 118/120 的近满分成绩。虽然前路仍长，但这些结果首次表明——可自证的数学推理不仅可行，更是通往更强数学 AI 的必由之路。

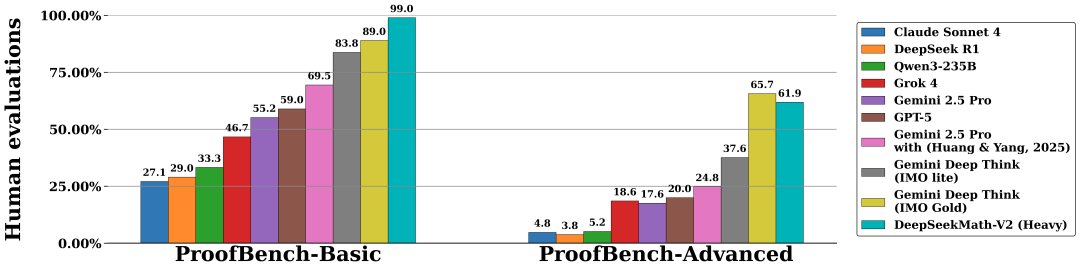
为什么“答对”不等于“会证”？

过去一年，大模型靠「最终答案奖励」把 AIME、HMMT 等竞赛刷到饱和，但

• 答对≠推理对：模型可能靠“蒙”或“跳步”拿到正确答案；
• 定理证明无“标答”：很多题目要的是严谨推导而非数值结果，传统奖励机制直接失效。

DeepSeekMath-V2 的目标：让模型像数学家一样，自己写证明、自己挑毛病、自己改到无懈可击。

方法概览：一条「生成-验证」双向增强飞轮

角色	模型	作用
证明生成器 πθ	基于 DeepSeek-V3.2-Exp	写自然语言证明
证明验证器 πφ	同尺寸 LLM	给证明打分、指出漏洞
元验证器 πη	同上	检查验证器有没有“幻觉”挑错

三者组成一个可扩展的强化学习闭环：

1. 用验证器当奖励模型，训练生成器写出更高分证明；
2. 生成器变强后，产出更难验证的新证明，反向成为验证器的“练兵场”；
3. 元验证器确保“挑错”本身可信，防止验证器靠 hallucination 拿高分。

核心组件拆解

3.1 验证器：如何训练一个“数学老师”？

• 数据：17 K 道 AoPS 竞赛题 + 多轮迭代生成证明，人工按 0/0.5/1 三档打分。
• 奖励：
• R_format：必须输出“Here is my evaluation …”+ \boxed{score} 格式；
• R_score：预测分与人工分越近奖励越高。
• 缺陷：早期验证器会“编漏洞”骗高分 → 引入元验证器。

3.2 元验证器：给“老师”再配一个“督导”

• 任务：检查验证器指出的漏洞是否真的存在、评分是否合理。
• 数据：专家对 1 K 份验证器输出再打分 → 训练 πη。
• 效果：验证器分析质量从 0.85 → 0.96，幻觉漏洞大幅下降。

3.3 生成器：学会“自我反省”

训练时要求一次输出两段：

##Solution
……（证明正文）
##SelfEvaluation
Here is my evaluation of the solution: …
\boxed{score}

奖励设计：

• R_Y：外部验证器给证明的真实分；
• R_Z：元验证器给“自评”的准确度分；
• 权重 α=0.76，β=0.24 →诚实认错比盲目自信更赚。

3.4 自动扩数据：人类标注退场

当验证器 & 元验证器足够强，用“多数元验证一致”原则自动给新证明打标签；
最近两轮训练完全取消人工标注，专家抽测一致性>96%。

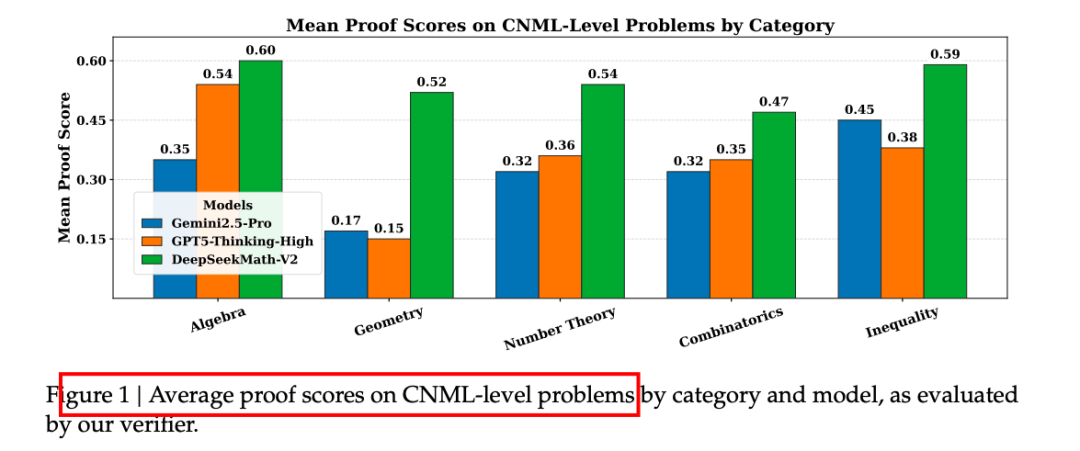
实验：竞赛级表现

比赛	题目数	DeepSeekMath-V2 得分	人类最佳
IMO 2025	6	83.3 %（5 题全对 + 1 题部分）	金牌线≈80 %
CMO 2024	6	73.8 %（4 全对 + 1 部分）	金牌线≈70 %
Putnam 2024	12	118/120	90/120

4.1 一步生成 vs 迭代精修

• CNML 难度：一步生成即全面领先 GPT-5-Thinking-High、Gemini-2.5-Pro；
• IMO-Shortlist：允许最多 8 次迭代后，Best@32 提升 **+15 %**。

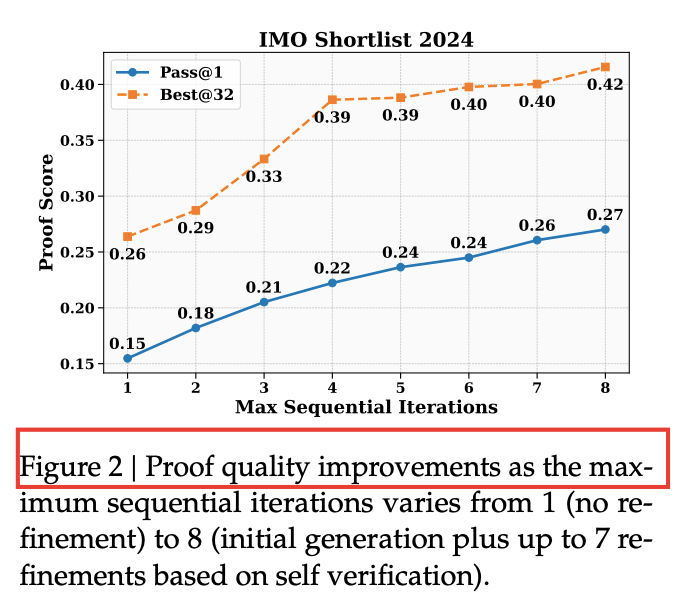
4.2 高算力搜索：64×64 并行“围剿”难题

• 每题维持 64 份候选证明 + 64 份验证分析；
• 16 轮迭代后仍无漏洞→视为解决；
• 11/12 道 Putnam 题被完全攻克，剩余 1 道仅微小瑕疵。

https://github.com/deepseek-ai/DeepSeek-Math-V2/blob/main/DeepSeekMath_V2.pdf
https://hf-mirror.com/deepseek-ai/DeepSeek-Math-V2
DeepSeekMath-V2: Towards Self-Verifiable Mathematical Reasoning
DeepSeek