|
ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.1em;color: rgb(63, 63, 63);text-align: left;">2023年，大模型如雨后春笋般爆发，58同城TEG-AI Lab作为AI平台部门，紧跟大语言模型技术发展步伐，打造了大语言模型平台，支持大语言模型训练和推理部署，并基于大语言模型平台构建了58同城生活服务领域（房产、招聘、汽车、黄页）垂类大模型灵犀大语言模型（ChatLing），支撑了业务方大模型应用的探索落地。灵犀大语言模型在公开评测集和实际应用场景下，效果均优于开源通用大语言模型以及商用通用大语言模型。 
ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.1em;color: rgb(63, 63, 63);text-align: left;">在研发灵犀大模型过程中，我们在大模型参数高效微调PEFT（Parameter-Efficient-FineTuning）上进行了广泛实践。本文系统性地解析了几种常用的大模型参数高效微调（PEFT）方法，并对每种方法的算法原理和应用效果进行了详细介绍。首先本文将阐述参数高效微调的重要性和基本概念，随后简要介绍LoRA微调之前的两种PEFT方法Adapter Tuning和Prefix Tuning，然后本文会详细介绍LoRA（Low-Rank Adaptation）、QLoRA（Quantized LoRA）和AdaLoRA（Adaptive Low-Rank Adaptor）以及SoRA（Sparse low rank adaptation）四种参数高效方法。这些方法旨在减少训练参数量、降低微调成本，同时保持模型性能。此外，本文还将分享基于Unsloth的微调加速实践经验，并且展示了在不同模型和数据集上的训练加速效果和显存占用降低效果。综上，本文将从微调方法和训练加速两个角度分享相关的技术解析和实践经验。ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;display: table;border-bottom: 2px solid rgb(15, 76, 129);color: rgb(63, 63, 63);">参数高效微调（PEFT）ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.1em;color: rgb(63, 63, 63);text-align: left;">自ChatGPT走红以来，众多厂商纷纷投身于人工智能大型语言模型的研发与应用。然而，高昂的计算成本使得从零开始训练一个大型语言模型对许多人而言是难以企及的。因此，自Transformer和BERT时代起，微调（fine-tuning）技术因其亲民性而受到青睐。对于业务应用而言，基于开源模型在大量语料上训练的语言模型，再针对特定业务领域数据进行微调，这种成本效益更高的方法在当前阶段似乎更符合大多数公司的需求。微调技术指的是在一个已经训练好的模型（预训练模型）的基础上，通过特定的下游任务数据对其进行进一步训练，从而使模型能够更好地适应特定任务的需求。预训练模型如同一个高效的特征提取器，基于先前训练数据中积累的经验，能够提取出有效的特征，从而显著提升下游任务的训练效果和收敛速度。全参数微调是指在下游任务的训练过程中，对预训练模型的所有参数进行更新。如下图所示在微调过程中，权重矩阵中的每个参数（d*d个参数）都要参与更新。然而对于大规模语言模型而言，传统的全参数微调方法所需的计算资源和时间成本极其高昂。例如，最近发布的开源模型如LLaMA 3-70B、Qwen 1.5-110B和DeepSeek-V2等，这些模型的参数规模之大使得即使是进行微调普通用户也难以承受。 ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.1em;color: rgb(63, 63, 63);text-align: left;">但是，由于模型在预训练阶段已经见过足够多的数据，收获了足够的经验，因此我只要想办法给模型增加一个额外知识模块，让这个小模块去适配我的下游任务，模型主体保持不变（freeze）即可。这就称之为参数高效微调，这种方式显然可以大大降低训练参数量，也就降低了微调成本，而且大幅提高了微调效率。下面，本文将介绍几种广泛使用的高效微调方法。ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;display: table;background: rgb(15, 76, 129);color: rgb(255, 255, 255);">Adapter Tuning与Prefix TuningingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;border-left: 3px solid rgb(15, 76, 129);color: rgb(63, 63, 63);">Adapter TuningingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.1em;color: rgb(63, 63, 63);"> 2019 年，Adapter Tuning将 Adapter 引入 NLP 领域，作为全模型微调的一种替代方案。Adapter 主体架构如下图所示。图例中的左边是一层Transformer Layer结构，其中的Adapter是前文描述的“额外知识模块”；右边是Adatper的具体结构。在微调时，除了Adapter的部分，其余的参数都是被冻住的（freeze），这样能有效降低训练参数量。Adapter的内部架构不是本文所述的重点，这里就不再介绍了。但这样的结构设计存在一个显著劣势：添加了Adapter后，模型结构整体变的更深了，会增加推理时长。 ingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;border-left: 3px solid rgb(15, 76, 129);color: rgb(63, 63, 63);">Prefix TuningingFang SC", "Hiragino Sans GB", "Microsoft YaHei UI", "Microsoft YaHei", Arial, sans-serif;letter-spacing: 0.1em;color: rgb(63, 63, 63);text-align: left;">前缀微调（prefix-tunning），用于生成任务的轻量微调。前缀微调将一个连续的特定于任务的向量序列添加到输入，称之为前缀。与提示（prompt）不同的是，前缀完全由自由参数组成，与真正的 token 不对应。相比于传统的微调，前缀微调只优化了前缀。因此，我们只需要存储一个大型 Transformer 和已知任务特定前缀的副本，对每个额外任务产生非常小的开销。Prefix Tuning通过在输入数据前增加prefix前缀来给模型提供一些先验知识的方式来提升微调效果，提供prefix的长度在训练中是一个可调整的超参，在微调中，同样需要冻结住模型其余模块，只训练prefix相关的超参即可。 如上论文图给出的是gpt2模型 ，prefix的作用是引导模型提取x相关的信息，进而更好地生成y。例如，我们要做一个summarization的任务，那么经过微调后，我们希望prefix能引导模型去提取输入x中的核心信息做总结。但是这样也会导致模型输入的增加，增加计算量和推理时间，并且增加prefix难以保证训练效果。 LoRA（Low-Rank Adaptation）原理由于上面两种方法的劣势，我们希望找到一种方法既能像全参微调一样不增加额外输入或改变模型结构，又能大幅度减少训练参数量降低微调成本的方法。基于此LoRA（Low-Rank Adaptation，低秩适配器）第一个解决了这个问题。如下图是LoRA的整体架构，Lora通过在原始权重矩阵W的旁边新增一个旁路，这个旁路由低秩的两个矩阵 A 和 B 组成，这两个低秩矩阵组合用来近似模拟全参更新中的ΔW 增量矩阵。在训练过程中，我们冻结住原始预训练模型的权重 W ，只更新LoRA的两个低秩参数矩阵 A 和 B 。为了在训练的初始时刻能保证加了LoRA Adapter之后不影响原始模型的能力，我们分别使用高斯初始化和零初始化来初始化 A 和 B 。  假设原始权重矩阵的维度是 d×d，LoRA低秩矩阵A的维度设置为 r×d，矩阵B的维度为 d×r，这里我们冻结原始权重，相当于只更新增量权重。可以理解为我们先通过A矩阵进行一个降维操作，然后再使用B矩阵进行升维操作。这样微调的参数就从原来的 d×d 降低到了 2×d×r。因为一般设置的参数 r 会远小于 d，所以这里能大大降低训练参数量。在训练过程中，由于预训练权重 W 被冻结，仅对低秩矩阵 A 和 B 进行训练。因此，在保存LoRA训练的权重时，仅需保存参数量相对较小的低秩部分即可。训练时，GPU显存通常存储以下内容：输入数据、模型权重、模型的中间结果、梯度以及优化器状态。相比全参数微调方法，LoRA训练中输入数据部分显存占用不变。而因为原始权重也需要参与计算，因此模型权重和中间结果的占用也不变（增加的LoRA部分权重几乎可以忽略不计）。关于梯度的显存占用分析则相对复杂，以反向传播时 B 的梯度计算为例进行具体分析如下： h=Wx+BAx=Wmx∂B∂L=∂h∂L∂Wm∂h∂B∂Wm 考虑 B 梯度的前两项，梯度的维度和预训练权重的梯度相同，均为 d×d。然而，由于LoRA并不作用于模型的所有层，并且由于训练参数的减少，优化器状态的存储显著减少，因为通常像类似adam优化器需要存储一阶梯度和二阶动量，而且通常优化器状态中存储的都是fp32类型的值，所以这部分显存占用相比全参微调大大降低，总体上显著降低了显存的占用。在推理时，将LoRA权重与原始权重合并即 h=(W+BA)x 的方式得到与原始模型一样的结构。这意味着完全不需要改变模型的任何结构，微调后模型的推理参数量与原始模型参数量完全一致。且这种方式让我们可以根据不同的业务场景基于同一个基座模型训练不同的LoRA权重，然后在不同的应用上加载不同的LoRA权重，非常灵活，而且LoRA权重通常非常小，也很易于存储和加载。 LoRA特点总结： 实验LoRA现已在业界广泛应用于各个场景的微调任务，在诸多任务中都被验证是有效且可行的。我们也基于两个业务场景做了单一任务的微调实践。LoRA的原理在于增量矩阵ΔW 满足低秩假设, h=(W+ΔW)×x中的ΔW确实是一个低秩矩阵。如果不满足该假设，那么LoRA的分解就一定会有精度损失，而达不到最好的微调效果。因此需要在任务中需要选择合适的r，理论上说，针对复杂的任务可能需要更大的r，但是r的值越大，可训练的参数量就越大，训练时长和显存占用就会同时变得更大。一般来说增大r的值会取得更好的微调效果，但是也不是一定如此，对于简单任务的微调太大的训练参数反而会使模型训练容易过拟合而导致效果变差。因此在实验阶段我们在两个NLU业务数据集上对比了全参训练、以及不同大小的r的训练效果，同时为了证明微调的效果，我们还加入了使用GPT4 zero-shot做该任务的效果对比。实验基座模型采用qwen1.5-7b-base，我们分别对比全参微调、LoRA不同r的微调以及直接使用GPT4的效果对比（业务数据集2中“有效问题”指除了标签为“其它”的数据，“拒识”指标签为“其它”的数据）： NLU业务数据集1: | 指标 | Precision | Recall | F1-Score | | GPT4 | 63% | 58% | 59% | | 全参 | 89.96% | 85.53% | 87.68% | | LoRA（r=2） | 89.42% | 85.85% | 86.23% | | LoRA（r=8） | 89.54% | 86.32% | 86.44% |
NLU业务数据集2: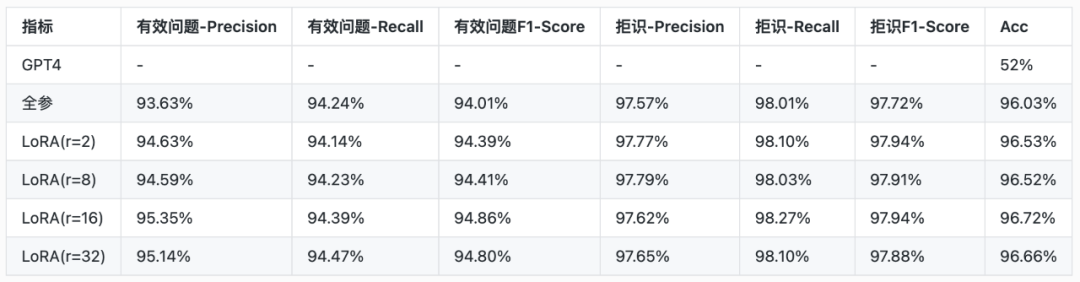 
由表中两个数据集的实验结果可见，在两个场景下，LoRA微调都达到了与全参微调媲美的效果，尤其在第二个场景，LoRA微调的效果实际比全参微调要更好。而且从第二个业务数据集的实验上看，LoRA微调的效果根据不同的秩的选取有较大关系，微调效果先随着秩的增大而变好，在秩为16时取得最好效果，随后继续增大则并没有提升。所以在用LoRA微调时，选取合适的秩的值非常重要。 QLoRA（Quantized LoRA）原理分位数量化和分块量化QLoRA的主要工作是通过模型量化进一步降低显存占用，从上文对LoRA原理的介绍中可以看到，LoRA微调是通过可训练参数的大幅降低从而显著降低了优化器状态部分的显存，模型权重和中间变量的显存占用实际上没有太大变化。而QLoRA通过定义了NF4的精度单位和双重量化方式将原始半精度的模型参数大小降低了数倍，从而进一步降低了训练时的显存占用。量化本质上把一群大数据范围的数舍入到用一群小数据范围的数来表示。举个简单例子我们把0-9的数用0-4来表示，那么显然0对应0，9对应4，而4和5可能都对应2，这就造成了量化误差，因为第一种数据中的4和5在第二种数据中都映射到了2，这就造成了信息的丢失，而这也就是量化误差的由来。这种误差是不可逆的，而诸多的量化方法，都只是为了尽可能减少这种误差，但是因为数据范围的减少，误差其实不可避免。为了尽可能减少量化误差，QLoRA结合了分位数量化和分块量化的技术。 分位数量化的思想来源于概率分布。由于模型的权重通常符合正态分布，通过利用这种分布特性可以有效降低量化误差。例如，在分布的两端，由于数据出现的概率较低，可以扩大映射的空间；而在分布的中间，由于数据出现的概率较高，可以压缩映射的空间。举例来说，假设原始数据类型为0-9且符合正态分布，需要用0-4来表示这些数据。在这种情况下，可以采用如下映射方案：将0-3映射为0，4映射为1，5映射为2，6映射为3，7-9映射为4。可以看到，分布中间的几个数实际上是无损量化的，而量化误差集中在分布的两侧。由于正态分布的特性，位于两侧的数据出现频率较低，因此这种量化方式可以有效降低整体量化误差。上述例子主要用于帮助读者理解这种量化方法的基本原理。实际上，在具体应用中需要借助数学上的累积分布函数来确定合适的“分位数”点。以4bit量化为例，共有4个bit位可用于量化数据，因此4bit量化将数据映射成16个数。4bit量化的关键在于找到这16个合适的分位点，从而确保量化过程高效且精确。而0对于神经网络权重来说通常具有特殊意义，所以我们希望保留0的位置，使得0被量化完之后还能映射到0位置，而且由于标准正态分布的0和1对应的累积分布函数的反函数的解为∞到−∞，因此我们需要提供一个offset偏移量，把范围从[0,1]缩减到[offset, 1-offset]。这就是分位数量化的主要思想，下面基于代码来简单介绍一下量化过程。 fromscipy.statsimportnorm
importtorch
defcreate_normal_map(offset=0.9677083,use_extra_value=True):
ifuse_extra_value:
#onemorepositivevalue,thisisanasymmetrictype
v1=norm.ppf(torch.linspace(offset,0.5,9)[:-1]).tolist()#正数部分
v2=[0]*(16-15)##wehave15non-zerovaluesinthisdatatype
v3=(-norm.ppf(torch.linspace(offset,0.5,8)[:-1])).tolist()#负数部分
v=v1+v2+v3
else:
v1=norm.ppf(torch.linspace(offset,0.5,8)[:-1]).tolist()
v2=[0]*(16-14)##wehave14non-zerovaluesinthisdatatype
v3=(-norm.ppf(torch.linspace(offset,0.5,8)[:-1])).tolist()
v=v1+v2+v3
values=torch.Tensor(v)
values=values.sort().values
values/=values.max()
assertvalues.numel()==256
returnvalues
Q=create_normal_map()
注意代码中的offset可能与上文介绍的略有不同，但目的是为了避免取到−∞和+∞。use_extra_value则是为了区分对称量化和非对称量化。如果use_extra_value为true则0左边将有7个值，0右边将有8个值，加上0共有16个值。而如果use_extra_value为false，则0的左右两边都有7个值，0占2个值。代码逻辑如下，先通过torch.linspace均匀取到offset到 0.5 的8个数。（为什么是0.5，因为标准正态分布，0位置对应的累积分布概率是0.5）。然后通过scipy.stats包的norm.ppf方法取到对应点的分位数值，再加上0位置对应的0，然后经过归一化操作之后，得到4bit量化的16个量化分位数。 分块量化，它的思想是把量化前的数据分成几个块，每个块的数据在每个块内量化，这样能尽可能降低整个数据中离群值对量化效果的影响。每个量化的块记录自己的量化常数，量化常数的计算方式是该块中数据的最大值，因为需要基于该量化常数计算归一化之后的值，然后根据最接近该值的分位数索引得到量化后的值。反量化时，只需基于该索引值找到量化分位数，再乘上对应的量化常数得到反量化结果。 双重量化和分页优化在上面分位数量化和分块量化中提到，模型不仅需要保存量化后的结果，还需要保存每个块的量化常数，而量化常数通常是全精度或半精度的即32位或16位。QLoRA的双重量化就是对这个量化常数再做一次8bit的量化，在进行量化常数的量化时，QLoRA以每256个量化常数为一组再做一次量化。因为使用了双重量化，在进行反量化时我们也需要进行两次反量化才能把量化后的值还原。最后分页优化是针对梯度检查点做的进一步优化，以防止在显存使用峰值时发生显存OOM的问题。QLoRA分页优化其实就是当显存不足时，将保存的部分梯度检查点转移到CPU内存上，和计算机的内存数据转移到硬盘上的常规内存分页一个道理。关于梯度检查点的内容不是本文重点要介绍的内容，因此这里不展开讲解。结合分位数量化、分块量化、双重量化和分页优化，QLoRA实现了极低的显存占用微调，而且与原始LoRA相比可以做到几乎不损失微调精度。即便是与全参微调相比，许多工作也证明QLoRA的精度损失极小，在工业界也广泛应用于许多场景的微调中。 实验NLU业务数据集1: 在一张A800上对Qwen1.5-7B进行QLoRA训练，使用相同的数据集训练5400个step，开启gradient_checkpointing，并在在所有linear层均插入lora adapter。结果显示QLoRA显著降低了显存占用，而且相比原始LoRA微调几乎没有性能下降，但是QLoRA由于需要额外的量化和反量化时间，因此训练时间会比普通LoRA略长。 | 指标 | 训练显存占用 | 训练时间 | | QLoRA | 39.1GB | 8760s | | LoRA | 55.7GB | 7192s |
| 指标 | Precision | Recall | F1-Score | | GPT4 | 63% | 58% | 59% | | 全参 | 89.96% | 85.53% | 86.68% | | QLoRA | 89.42% | 85.85% | 86.23% | | LoRA | 89.54% | 86.32% | 86.44% |
AdaLoRA（Adaptive Low Rank Adaptor）原理在LoRA（Low-Rank Adapted）的介绍中提到，通过添加一个低秩的适配器旁路，LoRA大幅度降低了微调参数量和显存占用。然而，LoRA中超参数 ( r ) 的设置是全局统一的，即在所有模块中采用相同的秩。这种做法显然无法满足不同模块的权重增量ΔW具有不同秩的实际情况。因此，从理论角度看，根据不同模块在模型中的重要性来设置不同的秩是更为合理的方法。为了解决这一问题，AdaLoRA（Adaptive Low-Rank Adapter）提出了一种对每个模块的秩进行自适应调整的方法。具体来说，AdaLoRA基于奇异值分解（SVD）的形式对ΔW 进行参数化更新。通过这种基于SVD的方法，AdaLoRA可以在避免复杂SVD计算的情况下，高效地裁剪不重要的奇异值，从而降低计算量达到高效微调的目的。SVD（Singular Value Decomposition）是传统机器学习一个重要的算法，它可以用在矩阵分解中，svd分解一个最重要的性质就是可以通过前k个奇异值和它对应的左右奇艺向量来近似表示原始矩阵，所以它经常被用于降维算法中。SVD分解可以表示为 A=UΣVT 其中 ? 和 ? 都是幺正矩阵（Unitary Matrix），即 UTU=IVTV=I 其中幺正矩阵是正交矩阵在复数上的推广。? 是 ? 的奇异矩阵，它是一个对角矩阵，对角线位置上的值是矩阵 ? 的奇异值。因为在一个模型中，不同模块拥有着不同的贡献，那么在使用LoRA时如果能够根据它们重要性的不同为不同的模块分配不同的秩，那么将会带来很多好处。首先，为重要性更低的模块分配更小的秩将有效的减少模型的计算量。其次，如果能够为更重要的特征分配更大的秩，那么将能够更有效的捕捉特征的细节信息。这也就是AdaLoRA的提出动机。为了实现这个目的，需要解决的问题有： 1. 如何融合SVD和LoRA？ 2. 如何建模参数的重要性？ 3. 如何根据重要性自动计算 ( r ) 的值？
融合SVD和LoRAAdaLoRA 将 LoRA 的两项式替换为 SVD 的三项式，AdaLoRA 的计算方式如下： W=W+ΔW=W+PΛQ 其中P和Q都是正交矩阵、Λ为对角矩阵。这样就完美的把 LoRA 的结构改造成了 SVD 分解中三项的形式。为了让分解的三项确实满足 SVD 分解的性质，AdaLoRA 在损失函数中加入了对P和Q的约束强制让P和Q满足正交矩阵的性质。 R(P,Q)=∣PTP−I∣F2+∣QQT−I∣F2 其中I代表单位矩阵。而因为P、Q中间的Λ是对角矩阵，所以可以用向量来存储节约空间。下面代码示例是PEFT库的AdaLoRA实现，清晰展示了AdaLoRA layer的结构： self.lora_A[adapter_name]=nn.Parameter(torch.randn(r,self.in_features))
#Singularvalues
self.lora_E[adapter_name]=nn.Parameter(torch.randn(r,1))
#Leftsingularvectors
self.lora_B[adapter_name]=nn.Parameter(torch.randn(self.out_features,r))
代码中的r是预先定义的超参，即初始的r，跟LoRA中的r是一个意思，矩阵A的维度是r×d，E矩阵是一个r×1的向量，这个代表SVD分解中的对角阵，B的维度是d×r。 下面代码块展示的是AdaLoRA在loss中加入对正交矩阵的限制代码，可以看到AdaLoRA在loss中加入了ppT−I的Fro范数，最小化该loss就可以让ppT接近单位矩阵，满足SVD分解正交的性质。根据上面介绍的模型结构和loss函数的设计，SVD分解就完美的和LoRA低秩分解结合在了一起。 forn,pinself.model.named_parameters():
if("lora_A"innor"lora_B"inn)andself.trainable_adapter_nameinn:
para_cov=p@p.Tif"lora_A"innelsep.T@p
I=torch.eye(*para_cov.size(),out=torch.empty_like(para_cov))
I.requires_grad=False
num_param+=1
regu_loss+=torch.norm(para_cov-I,p="fro")
ifnum_param>0:
regu_loss=regu_loss/num_param
else:
regu_loss=0
outputs.loss+=orth_reg_weight*regu_loss
计算参数重要性AdaLoRA中，我们把LoRA低秩分解和SVD分解结合在了一起，分解的形式是PΛQ，如下图，基于此我们可以根据P，Q矩阵中的奇异向量和Λ中的奇异值组成的三元组，来把重要性高的三元组留下，丢弃重要性低的三元组。通过将重要性低的三元组置为0来设置各个模块的r，也就达到了AdaLoRA最初的目的，解决LoRA中所有模块的秩都相同的问题。  重要性分数通过敏感性（Sensitivity）和不确定性（Uncertainty）两个方面进行计算。在计算敏感性时，对于单个参数，采用该参数的权重与其梯度绝对值的乘积作为敏感性值。由于权重和梯度是训练时在当前批次数据中的值，可能在不同批次间存在较大差异，因此对其施加滑动平均操作，记录整个训练过程中的滑动平均值作为敏感性分数。另外，还需要计算不确定性分数，用以衡量参数在训练过程中敏感性的波动情况。某一时刻的不确定性分数通过该时刻的敏感性分数减去到该时刻为止的敏感性分数的滑动平均值得到，用以评估参数变化幅度。最终，对不确定性分数也同样施加滑动平均操作，得到最后的不确定性分数。以下为相关关键代码的部分片段。 defupdate_ipt(self,model):
#Updatethesensitivityanduncertaintyforeveryweight
forn,pinmodel.named_parameters():
if"lora_"innandself.adapter_nameinn:
ifnnotinself.ipt:
self.ipt[n]=torch.zeros_like(p)
self.exp_avg_ipt[n]=torch.zeros_like(p)
self.exp_avg_unc[n]=torch.zeros_like(p)
withtorch.no_grad():
self.ipt[n]=(p*p.grad).abs().detach()
#Sensitivitysmoothing
self.exp_avg_ipt[n]=self.beta1*self.exp_avg_ipt[n]+(1-self.beta1)*self.ipt[n]
#Uncertaintyquantification
self.exp_avg_unc[n]=(
self.beta2*self.exp_avg_unc[n]+(1-self.beta2)*(self.ipt[n]-self.exp_avg_ipt[n]).abs()
)
最后用敏感性分数和不确定性分数的乘积来表示该参数的重要性分数。而对于三元组Pi，σi，Qi来说，三元组的重要性分数就等于三元组三个值的加权和。 def_element_score(self,n):
returnself.exp_avg_ipt[n]*self.exp_avg_unc[n]
根据重要性自动计算秩?的值在获得AdaLoRA中每对三元组的重要性分数后，可以根据这些分数确定每个模块的r值。在奇异值分解（SVD）中，特征的重要性取决于其对应奇异值的绝对值大小。基于这一思想，AdaLoRA采用了一种剪枝策略，即根据Λ中λ的值，将不重要的元素置0，而重要的元素则使用Λk(t)的值进行替换。由于这一策略不涉及矩阵大小的修改，因此Λ始终保持在r×r的大小。在AdaLoRA的超参数中，需要定义初始秩initr和最终秩targetr。在训练中，模型会逐步根据三元组的重要性分数，仅保留重要性高的三元组，而将不重要的置0。通过这种方式，初始秩最后将降低到最终秩。然而，模型中每一层的AdaLoRA模块的秩r值并不一定都降到最终秩。例如，如果在模型的10个层上添加AdaLoRA适配器，并设置初始秩为16，最终秩为8，则初始的三元组总数为10×16=160。在训练过程中，会根据各个三元组的重要性分数保留前10×8=80个（剩下的80个三元组置0）。具体实现的关键代码如下： all_score=[]
#取到每个三元组的重要性分数
#Calculatethescoreforeachtriplet
forname_minvector_ipt:
ipt_E=value_ipt[name_m]
ipt_AB=torch.cat(vector_ipt[name_m],dim=1)
#
sum_ipt=self._combine_ipt(ipt_E,ipt_AB)
name_E=name_m%"lora_E"
triplet_ipt[name_E]=sum_ipt.view(-1,1)
all_score.append(sum_ipt.view(-1))
#取到前budget个数的分数值做为mask的threshold阈值
#Getthethresholdbyrankingipt
mask_threshold=torch.kthvalue(
torch.cat(all_score),
k=self.init_bgt-budget,
)[0].item()
rank_pattern={}
#直接把小于threshold阈值的三元组置0
#Masktheunimportanttriplets
withtorch.no_grad():
forn,pinmodel.named_parameters():
iff"lora_E.{self.adapter_name}"inn:
p.masked_fill_(triplet_ipt[n]<=mask_threshold,0.0)
rank_pattern[n]=(~(triplet_ipt[n]<=mask_threshold)).view(-1).tolist()
returnrank_pattern
至此，AdaLoRA的基本原理已全面介绍完毕。接下来还需讨论的一个问题是：如何确定在当前训练时刻需要保留多少三元组，以及mask掉多少三元组，即如何确定上文代码中的budget值。实际上，这里使用了一种类似于深度学习中的warm-up机制。以下是计算budget的具体过程，需要用到AdaLoRA的两个超参数，分别是tinit和tfinal。这两个超参数的含义都是训练步数。具体而言，在前tinit步内，AdaLoRA使用初始秩initr，即不改变矩阵的秩，以便模型在早期阶段达成相对稳定的效果；在最后的tfinal步内，AdaLoRA的秩等于设置的最终秩targetr。中间的训练步数，则以三次方幅度使budget值从初始值initr逐渐减小到目标值targetr。 defbudget_schedule(self,step:int):
tinit=self.peft_config.tinit
tfinal=self.peft_config.tfinal
total_step=self.peft_config.total_step
#Initialwarmup
ifstep<=tinit:
budget=self.init_bgt
mask_ind=False
#Finalfine-tuning
elifstep>total_step-tfinal:
budget=self.target_bgt
mask_ind=True
else:
#Budgetdecreasingwithacubicscheduler
mul_coeff=1-(step-tinit)/(total_step-tfinal-tinit)
budget=int((self.init_bgt-self.target_bgt)*(mul_coeff**3)+self.target_bgt)
mask_ind=Trueifstep%self.peft_config.deltaT==0elseFalse
returnbudget,mask_ind
AdaLoRA相比LoRA有更多的公式推导和计算逻辑，介绍起来感觉比较复杂，它的流程可以用下面原论文中的流程图来概括 
实验使用AdaLoRA训练在transformers库的traininer脚本中需要做改动的地方有 ifself.rankallocatorisnotNone:
self.rankallocator.set_total_step(max_steps)
optimizer.step()
lr_scheduler.step()
#Updatetheimportanceoflow-rankmatrices
#andallocatethebudgetaccordingly.
model.base_model.update_and_allocate(global_step)
实验结果我们在NLU业务数据集1上同样基于qwen1.5-7B模型对比了AdaLoRA和LoRA微调的效果，尝试了几组超参实验，都未能取得较好效果，相比LoRA微调在该场景下具有一定的性能差距（表中给出的adalora的r值设定已经尝试过的最好结果）。基于该实验结果，我们怀疑是AdaLoRA的正定假设有点过于严苛，在损失函数中加入如此严格的设定，可能限制了模型的效果。但是AdaLoRA对于改变不同模块秩的思路非常有价值，后续仍有很多基于该思路的优质工作。 NLU业务数据集1: | 指标 | Precision | Recall | F1-Score | | lora（r=2) | 89.42% | 85.85% | 86.23% | | lora(r=8) | 89.54% | 86.32% | 86.44% | | adalora (r=2) | 86.28% | 81.84% | 82.37% |
SoRA（Sparse low rank adaptation）原理在前文中，已经详细介绍了LoRA和AdaLoRA的高效微调方法。尽管LoRA展示出了卓越的性能，但是它每个模块的秩都是固定且不可更改的，这在某些应用场景中可能并不理想。相比之下，AdaLoRA通过基于参数的重要性进行剪枝从而赋予不同模块不同的秩来解决该问题。然而，这种方法的假设较为严格，因为其在损失函数中加入了对于正交性的严格限制，这在一定程度上可能会影响模型效果。为此，SoRA提出了一种创新的动态调整秩的方法。在训练阶段，SoRA通过引入基于近端梯度法优化的门单元，实现在门的稀疏性下控制秩的大小。这种方法在推理阶段，通过消除与归零后的秩相对应的参数，使每个SoRA模块缩减回简洁但性能优异的LoRA模块，从而在保证模型效率的同时提高了灵活性和适应性。如下图是论文中对SoRA结构的示意图：  SoRA在普通LoRA的低秩分解中间加了一个门单元g，图中也可以看到，输入X先经过一个降维矩阵Wd，变成h，再经过门单元g控制Wd的秩（控制秩的操作在于门单元g部分值为0），类似于把Wd的某一行全部置为0，这个操作与adalora相比是自适应的，也就是不需要手动设置target r预算并根据阈值置0。门操作的更新函数如下：（这样设置的原因其实是因为这是求近端梯度下降算法LASSO问题的解析解：软阈值函数） gt+1←T(gt,λ) 其中 Tλ(x):=⎩⎨⎧x−λ,0,x+λ,x>λ−λ<x≤λx≤−λ SoRA模块的结构代码如下： definit(self,...):
...#省略
ifr>0:
self.lora_A=nn.Parameter(weight.new_zeros((r,in_features)))
self.lora_B=nn.Parameter(weight.new_zeros((out_features,r)))
self.gate=nn.Parameter(torch.randn(1,r))
self.scaling=self.lora_alpha/self.r
nn.init.kaiming_uniform_(self.lora_A,a=math.sqrt(5))
nn.init.zeros_(self.lora_B)
defforward(self,x):
return((self.lora_dropout(x)@self.lora_A.T).mul(self.gate)@self.lora_B.T)*self.scaling
而且上面提到的更新gate值的操作是在优化器optimizer优化的step函数中进行的，因为gate参数并不需要通过传统的梯度下降来更新。其中关键代码片段摘抄如下，其中sparse_lambda是一个超参数。 #p.data代表gate的值sparse_lambda是一个超参
ifself.sparse_lambda>0:
p.data[p.data>self.sparse_lambda]-=self.sparse_lambda
p.data[p.data<-self.sparse_lambda]+=self.sparse_lambda
p.data[abs(p.data)<self.sparse_lambda]=0.0
这就完成了上面介绍的门单元参数更新的函数，此外，我们需要在损失中加入sparse gate门单元的损失，等于gate参数的1范数，加这个是由于求解近端梯度下降算法需要。关键代码如下： ifself.args.train_sparse:
sparse_loss=0.0
p_total=0
forn,pinmodel.named_parameters():
if"lora.gate"inn:
sparse_loss+=torch.sum(torch.abs(p))
p_total+=torch.numel(p.data)
loss+=self.sparse_lambda*sparse_loss/p_total
实验我们在2个NLU业务数据集上基于qwen1.5-7B模型对比了SoRA、AdaLoRA和LoRA微调的效果，尝试了几组超参实验，得到的实验结果显示SoRA微调在两个业务场景下都有很好效果。尤其在第二个业务场景，每个指标都取得了最好效果。 NLU业务数据集1: | 指标 | Precision | Recall | F1-Score | | LoRA | 89.54% | 86.32% | 86.44% | | AdaLoRA | 86.28% | 81.84% | 82.37% | | SoRA | 89.81% | 86.08% | 86.52% |
NLU业务数据集2: 
微调加速实践前文已经介绍了几种高效低参微调方法，这些方法在微调任务中能够有效节省训练资源并加快训练速度。高效率微调的方法可以通过使用低参数的微调策略来节约显存和计算量，同时也可以通过优化训练过程以加速训练。结合这两方面的方法，可以使微调训练任务更高效，在节约训练资源的前提下更快速地观测到微调效果。下文将分享利用大模型训练加速工具Unsloth进行加速实验的相关实践尝试。 UnslothUnsloth通过使用优化过反向传播的模块来覆盖大模型modeling的某些module来加速训练。这一过程通过手动实现反向传播步骤，将原始的PyTorch模块用Triton内核重写。Unsloth不仅能够减少内存使用，还可以加快微调速度，并且相较于常规的LoRA或QLoRA，精度下降为0%。具体而言，Unsloth采用OpenAI的Triton语言，重写了如RoPE、MLP和LayerNorms等结构的前向传播及反向传播方法，优化了GPU的计算性能和显存占用。由于现代大型语言模型通常拥有非常深的结构，例如LLaMA通常包含32个甚至更多层级，因此在反向传播过程中需要计算大量参数的导数作为中间变量，并且需要执行非常深层次的链式求导。在LoRA微调过程中，LoRA层的维度可能为8到128，但LLaMA结构的维度通常是1024的倍数，甚至达到4096。Unsloth加速机制的核心在于优化这种具有大维度变化的链式矩阵求导计算，并且在梯度计算和更新过程中，广泛使用inplace操作，从而进一步降低显存占用。 微调加速改动方式如下：使用unsloth包的FastLanguageModel的FastLanguageModel.get_peft_model方法替代peft包的get_peft_model方法即可。 fromunslothimportFastLanguageModel
ifmodel_args.use_unsloth:
fromunslothimportFastLanguageModel#type:ignore
unsloth_peft_kwargs={
"model":model,
"max_seq_length":model_args.model_max_length,
"use_gradient_checkpointing":"unsloth",
}
model=FastLanguageModel.get_peft_model(**peft_kwargs,**unsloth_peft_kwargs)
else:
lora_config=LoraConfig(
task_type=TaskType.CAUSAL_LM,
inference_mode=False,
use_dora=finetuning_args.use_dora,
**peft_kwargs,
)
model=get_peft_model(model,lora_config)
测试结果目前测试结果在qwen1.5和llama3下均有较明显的训练加速和显存占用降低的效果 我们在两个场景的lora微调下使用一张A800测试了加速效果，qwen和llama系列能有效降低训练时长30%左右，提升训练速度40%左右，且能降低显存占用40%+。如果使用4bit的qlora微调，则能进一步降低显存占用到极低水平。 NLU业务数据集2: | 指标 | flash-attn | unsloth | 加速效果 | qwen-7b
(batchsize=4) | 13.67h | 9.67h | train_time -29.3%｜train_speed 1.41X | qwen-7b
(batchsize=16) | 12h | 7.75h | train_time -35.41%｜train_speed 1.55X | qwen1.5-7b
(batchsize=4) | 13.7h | 9.67h | train_time -29.3%｜train_speed 1.41X | qwen1.5-7b
(batchsize=16) | 12.1h | 7.76h | train_time -35.8%｜train_speed 1.56X |
（注：因该数据集较大，训练时间较长，训练时长为根据前1000step的训练时长预估的总训练时长，可能跟实际总训练时长略有出入。） NLU业务数据集1：7412条数据训练、3个epoch、batch_size为4，共5559个step的条件下测试结果如下（完整训练参数附在最后）： •训练加速效果对比
Model ：qwen1.5-7b / llama3-8b / qwen1.5-14b 加速方法：none指原生transformers库的trainer，不含其它加速方法 / 启用flash-atten tion / 启用unsloth / 同时启用flash-attention和unsloth
| 指标 | none（transformers） | flash-attn | unsloth | unsloth+flash-attn | 加速效果 | | qwen-1.5-7b | 2.1h | 1.9h | 1.5h | 1.5h | 训练时间 -28.5%｜训练速度 1.42X | | llama3-8b | 2.79h | - | 2.1h | 2.1h | 训练时间 -24.7%｜训练速度 1.33X | | qwen-1.5-14b | 3.44h | - | 2.76h | 2.74h | 训练时间 -20.3%｜训练速度 1.25X |
| 指标 | none（transformers） | flash-attn | unsloth | unsloth+flash-attn | 降低显存占用效果 | | qwen-1.5-7b | 72GB | 72Gb | 39.2GB | 39.2GB | 显存占用 -45.56% | | llama3-8b | 68.8GB | - | - | 36.6GB | 显存占用 -46.8% | | qwen-1.5-14b | 78.8GB | - | - | 51.8GB | 显存占用 -34.26% |
总结本文详细介绍了几种高效微调方法的原理解析和实验效果对比，并基于Unsloth做了一些微调加速的实践尝试。实验效果显示结合优秀的低参微调方法和微调加速，完全可以做到极为高效的微调大模型，可以在极低的资源占用上得到媲美全参微调的效果。 | 
